academie-gaullisme865

L’ÉCOLE POLYTECHNIQUE ET LA SCIENCE DE L’ÉDUCATION RÉPUBLICAINE

(Quatrième partie)

par Jean-Louis GUIGNARD

L’histoire de la Révolution française a été si mystifiée que les simples « droits démocratiques » et la « liberté » dont jouissent aujourd’hui les citoyens de France et des autres nations capitalistes européennes passent pour la principale conquête de cette période révolutionnaire, une conquête que nous devrions aux Jacobins, aux Sans-culottes et à la prise de la Bastille. Il est grand temps de démonter la supercherie et de jeter aux poubelles de l’histoire ces instruments de la politique britannique, les Mirabeau, Danton et autres Marat tenus aujourd’hui encore pour les grandes figures de la Révolution française. II est surtout grand temps que les hommes qui ont, eux, dirigé l’authentique Révolution française, relégués à un rang secondaire de l’histoire ou enfouis plus profondément sous des calomnies, soient connus du grand public pour la contribution cruciale qu’ils ont faite au développement de la civilisation humaine.

Le texte qui suit a été initialement publié dans La science de l’éducation républicaine, Campaigner Publications, 1980.

La géométrie et la philosophie de la science

L’homme est à l’image de Dieu (un vrai chrétien aux yeux des Oratoriens) lorsqu’il tend vers son soi-perfectionnement en recherchant le perfectionnement de l’univers. Et Dieu, pour les Platoniciens et leurs héritiers, le principe créateur de la soi-perfection, était le Géomètre. « Que nul n’entre ici s’il n’est géomètre », Platon avait-il fait inscrire au-dessus de la porte de son Académie, car la géométrie, comme Monge, Carnot et Dupin le comprirent, est aussi la « philosophie de la science ».

C’est pourquoi la géométrie joua un si grand rôle dans la formation de la première génération de polytechniciens. Non pas en tant qu’ensemble fixe d’axiomes telle qu’elle est malheureusement enseignée couramment aujourd’hui, mais parce que cette branche de la science représente un moyen unique d’éduquer l’esprit à la raison en communiquant l’idée de la rationalité de l’univers physique et de la rationalité correspondante de l’esprit humain. Pour Monge, qui a contribué de manière cruciale au développement de cette science, l’objet de la géométrie résidait avant tout dans la manière dont les formes et les figures sont générées, dans l’évolution de leurs rapports au sein de configurations changeantes, et non dans leurs qualités fixes. Il cherchait avant tout à transmettre la notion du processus grâce auquel il était parvenu à ses découvertes géométriques, un processus qu’il ne manquait pas d’associer à un sentiment de joie profonde.

L’apport le plus connu de Monge est la « géométrie descriptive », c’est-à-dire, formellement, la représentation d’objets à trois dimensions dans un espace à deux dimensions. Selon cette méthode, chaque point de l’espace est représenté par ses projections orthogonales sur deux plans perpendiculaires ; le deuxième plan est ensuite censé être replié sur le premier par sa rotation autour de leur intersection, et les deux projections se trouvent ainsi sur le même plan horizontal. Les travaux de Monge dans ce domaine sont la prolongation directe de ceux réalisés un siècle auparavant par Descartes et le grand géomètre Desargues.

Avant Gaspard Monge, il n’existait aucune manière codifiée de représenter précisément sur un plan un objet à trois dimensions. On conçoit dès lors qu’il était très difficile de faire construire n’importe quelle machine, par plusieurs personnes, car les différentes pièces de la machine n’étaient plus ajustées. Ce problème devenait insurmontable dès qu’il fallait produire les différentes pièces dans plusieurs villes éloignées. C’est Monge qui avec la géométrie descriptive a créé le moyen de remédier à cette situation en systématisant une méthode de représentation d’un espace à trois dimensions dans le plan.

Soit un segment AB sur une droite D. La méthode consiste à projeter orthogonalement les extrémités A et B sur deux plans perpendiculaires notés P et Q. Les projections seront respectivement A’, B’ et A", B".

Il suffit de rabattre le plan Q sur le plan P’, prolongement du plan P, et de reporter alors les points A" et B" sur le plan P’, ce qui nous donne les points indiqués a et b. La représentation finale du segment AB est indiquée ci-dessous.

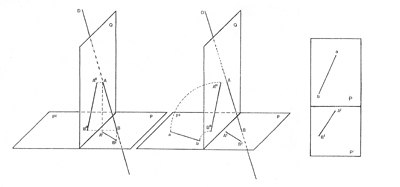
C’est cette méthode projective qui est à la base du dessin industriel et du dessin architectural.

Cette nouvelle branche de la géométrie fut le fruit du souci constant de Monge de développer l’industrie française, notamment la métallurgie et la mécanisation. Il savait que ce développement ne pouvait être amorcé qu’en appliquant aux différents domaines de la technologie des méthodes scientifiques. À l’époque, il existait une situation chaotique dans les divers secteurs techniques utilisant des méthodes graphiques, dans ce sens que leur efficacité générale était grandement entravée par de nombreuses divisions et particularités. Monge comprit que pour parvenir à une efficacité technique supérieure qui assurerait le progrès industriel, il fallait refondre les procédés existants disparates utilisés par les différentes techniques. C’est ainsi qu’il fit la synthèse d’un nouveau concept en mettant à jour le principe commun sous-jacent à toutes les techniques graphiques et à tous les problèmes liés à l’espace, et qu’il découvrit qu’en posant sous une forme géométrique les différents problèmes posés par les différentes techniques, une similarité allait apparaître qui permettrait de résoudre ces problèmes à l’aide de la méthode des deux projections orthogonales (8). La clé de son approche - approche que l’on retrouve par ailleurs dans tous les aspects de ses travaux - est que celle-ci est fondée sur le principe général du continuum développé par Leibniz. Au lieu de rechercher des solutions particulières aux différents problèmes qui se présentaient, il rechercha l’invariant qui pouvait résoudre ces différents problèmes en les situant dans un ordre de lois de mathématique physique supérieur. En fait, la géométrie descriptive était bien le moyen de parvenir à des ordres supérieurs de technologie, en permettant de traduire géométriquement la conception globale de réalisations techniques plus complexes qui requièrent une plus grande division du travail, en offrant « un langage nécessaire pour l’homme de génie qui conçoit un projet, pour ceux qui doivent en diriger la réalisation, et finalement, pour les artistes qui eux-mêmes doivent en réaliser les différentes parties », comme Monge l’explique dans l’introduction à son Traité sur la Géométrie Descriptive.

Monge commença à travailler sur cette idée vers 1775 et l’élabora durant toute la période où il enseigna à Mézières. Il présenta sa géométrie descriptive entièrement conceptualisée pour la première fois publiquement dans son cours à l’École normale en 1794. Lorsqu’il était professeur d’hydrodynamique à l’École du Louvres dans les années 1780, Monge réalisa de nombreuses études et expériences sur les machines hydrodynamiques, et il considérait que l’étude d’une « théorie des machines » devait faire partie intégrante de son cours sur la géométrie descriptive. Il avait entrepris une classification générale des machines (plus tard complétée par l’un de ses élèves et collaborateurs de l’École, Hachette), qui eut une grande influence sur les auteurs de traités de mécanique du XIXe siècle. Jusqu’à Monge, les milieux scientifiques n’avaient abordé l’étude des machines que du point de vue de la description de leurs détails ; Monge partit lui du principe de leur conception globale.

« Monge voulait qu’on appliquât cette géométrie à la description générale des machines, pour réduire ainsi qu’il en avait l’idée tous les moyens de transmettre de la force et du mouvement à des éléments parfaitement connus, classés et disponibles comme les instruments de l’atelier bien ordonné d’un excellent artiste. Il voulait enfin qu’on répandit par tous les moyens possibles, et qu’on rendit presque vulgaires à force de les populariser, la description et l’interprétation d’une foule de phénomènes de la nature, qui, par leur action, peuvent avoir une influence plus ou moins grande sur les travaux de notre industrie », écrivit Dupin.

Parmi les travaux les plus importants de Monge en géométrie, il faut noter ceux sur la génération des surfaces : Monge remarqua que les surfaces utilisées n’avaient généralement pas de degré défini, ce qui était au contraire fondamental c’était leur mode de génération. La réponse qu’il fit un jour à l’Ecole normale à un disciple de Condillac qui arguait que pour comprendre les éléments géométriques, il fallait suivre l’« ordre logique », solide, surface, ligne et point, est significative à cet égard. Monge montra que les surfaces développables contrairement aux objets fixes, sont des plus utiles pour la technique ainsi que pour la théorie des ombres et le processus de l’analyse, et insista sur l’importance de la classification des surfaces selon leur mode de génération : « Dire qu’une surface est de révolution, c’est donner l’idée de la manière dont elle a été engendrée ; c’est indiquer la grande famille dont elle fait partie ; c’est prouver qu’elle a toutes les propriétés qui conviennent à toute la famille en général », Monge expliqua-t-il. Dans les exercices qu’il donnait à ses élèves, Monge s’efforçait toujours de développer en eux un sens de l’intuition géométrique. « Il faut que l’élève se mette en état d’une part de pouvoir décrire en analyse tous les mouvements qu’il peut concevoir dans l’espace, et de l’autre, de se représenter perpétuellement dans l’espace le spectacle mouvant dont chacune des opérations analytiques est l’écriture », dit-il. Pour lui, comme pour Carnot et les « grands géomètres » qu’ils formèrent, il n’existait pas d’opposition entre l’analyse et la géométrie, qu’ils considéraient comme deux aspects complémentaires d’une même science mathématique. Le divorce entre l’analyse (algèbre) et la géométrie n’intervint que plus tard au XIXe siècle, et ouvrit la voie au « symbolisme algébrique » désastreux des « mathématiques modernes ». Monge soulignait en fait dans son enseignement de la géométrie, le lien entre le mode de génération des figures géométriques et celui de certains types de phénomènes physiques - lien qui a été essentiellement brisé par les mathématiques d’aujourd’hui.

« L’influence scientifique de Monge s’étendit bien au-delà des murs de son École et des frontières de son pays, et donna son élan au développement de la géométrie qui allait commencer en Allemagne. J’ai moi-même grandi, grâce à mon professeur Plücker, dans la tradition de Monge », a écrit le grand mathématicien Felix Klein, qui reprit cette tradition dans son Programme d’Erlangen, contre lequel Bertrand Russell, le père des mathématiques modernes, réagit quelques années plus tard en publiant ses Principia Mathematica.

Alors qu’on lui demandait un jour pourquoi il n’avait pas introduit directement la méthode des projections orthogonales dans son cours sur la géométrie descriptive, Monge répliqua qu’il fallait « suivre la marche naturelle de l’esprit ; il fallait vous montrer la nature du spectacle que l’on a toujours sous les yeux. Il fallait enfin exciter en vous quelques-unes des émotions que ce spectacle est propre à produire ; et si, parmi vous, il y en a un à qui, pendant la première leçon ou à la lecture de la première séance, le cœur ait battu, c’en est fait, il est géomètre ». Monge, et plus encore peut-être, Carnot et Dupin, savaient que l’essence de la géométrie, comme de toute science, ne tient pas au simple fait qu’elle est un instrument pour changer le monde mais au processus mental qui précède chez le savant la manipulation de l’instrument, grâce auquel celui-ci crée des hypothèses - dont Newton, lui, niait la nécessité - qu’il vérifie ensuite par la médiation de l’instrument scientifique.

C’est ce que Carnot a appelé « le génie lui-même », ce que Dupin a appelé « la philosophie de la science », ce qui « précède la marche matérielle des manipulations mathématiques », et ce que Platon a appelé « l’hypothèse supérieure ». C’est le principe grâce auquel l’individu créateur parvient au savoir réel, celui qui recouvre la connaissance des objets particuliers et des instruments particuliers qui nous aident à saisir les processus physiques ; le principe qui ordonne la succession d’hypothèses et qui a permis à l’homme d’atteindre des niveaux de savoir supérieurs à travers l’histoire platonicienne et néo-platonicienne.

Monge, Carnot, Dupin et leurs successeurs associaient consciem- ment ce processus à une émotion de joie, et, comme le dit si bien Monge, éprouver cette joie est la condition pour devenir un véritable géomètre, quelqu’un pour qui la géométrie va être le moyen de saisir le principe ordonnant de l’univers et non un corps fixe de Dupin savoir. En lisant ce que Carnot et Dupin disaient de cette géométrie supérieure (voir ci-dessous « Le charme insoupçonnable de la géométrie »), tout professeur de mathématiques honnête aujourd’hui devrait être confondu par le caractère destructeur des « maths modernes », ce pur produit du réductionnisme britannique qui, au lieu de susciter chez les enfants l’enthousiasme qui accompagne la découverte sensuelle de la rationalité de l’univers, anéantit et la rationalité et l’émotion de joie créatrice sous un flot de symboles abstraits et même absurdes.

Le charme insoupçonnable de la haute géométrie

Les personnes qui commencent à cultiver la haute géométrie, ne sauraient soupçonner le charme qu’elles éprouveront, un jour, à ce travail. Elles ne voient, dans les premiers rudiments de la science, qu’un enchaînement inextricable, de propositions abstraites, de démonstrations épineuses, de descriptions qui fatiguent et rebutent l’intelligence. C’est, en effet, une étude fort pénible que celle des premières conceptions de la géométrie à trois dimensions. Il faut apprendre à se représenter, en idée, des surfaces et des courbes dont les formes, d’une complication plus ou moins grande, sont variées à l’infini. Il faut les voir par les yeux de l’esprit, se couper, se toucher, s’envelopper, suivant des conditions données. Mais, quand ce travail intellectuel nous a rendus familiers avec les propriétés qui caractérisent les principales espèces de courbes et de surfaces, il semble qu’un nouvel ordre de conceptions vienne d’être créé dans notre entendement. Nous découvrons des rapports généraux, immuables, qui sont les lois éternelles de l’étendue figurée. Ces vérités mathématiques, loin d’être abstraites, se présentent à notre intelligence, sous des aspects visibles et pour ainsi dire palpables. Voilà comment l’imagination, qui semblait étrangère à des conceptions purement rationnelles, crée en quelque sorte un monde nouveau dont les objets, soumis dans leur position, dans leur figure et dans leurs mouvements, à des règles invariables, présentent de toutes parts, des idées d’ordre, de constance et d’harmonie.

« Lorsqu’ensuite nous passons de ce monde géométrique à la réalité du monde physique, nous retrouvons, dans les espaces que la matière occupe et dans les espaces qu’elle parcourt, les formes abstraites que la science avait imaginées. Les lois générales auxquelles sont assujetties ces abstractions mathématiques, reçoivent tour à tour leur application. L’esprit humain découvre, avec une surprise où le plaisir est égal à l’admiration, que l’univers et ses phénomènes portent dans leur existence, le type ineffaçable de ces formes idéales et de ces lois théoriques (…).

« Par ces hautes conceptions, l’Univers a cessé d’apparaître aux yeux des hommes, sous l’aspect incohérent des éléments de la matière, dispersés ou réunis, découverts ou cachés, par les caprices du hasard. L’intelligence humaine a connu par degrés qu’une géométrie sublime préside aux mouvements, aux formes, aux rapports de grandeur et de position de tous les corps célestes. Notre savoir s’est élevé, dans les applications d’une admirable théorie, jusqu’à connaître l’ensemble des parties figurées de l’espace qui furent, qui sont ou qui seront le lieu, le centre, ou l’axe, ou l’orbite, des mouvements perpétuels que suivent les grandes masses de notre système planétaire et leurs moindres éléments. Ainsi, dans l’espace et dans la durée, depuis l’infiniment petit jusqu’à l’infini, tout est soumis à des lois mathématiques.

« En méditant sur ces lois immuables et savantes, par lesquelles une Suprême Intelligence régit le temps et l’Univers, les sages n’ont pu trouver, pour l’appeler d’après ses œuvres, aucun titre plus juste et plus sublime, que celui de l’Eternel Géomètre. » Charles Dupin, Considérations générales sur les applications de la géométrie.

Ce n’est qu’en comprenant sensuellement ce « principe poétique » sous-jacent à la mentation créatrice dans les différents domaines de la science de même que dans le grand art, comme la poésie elle-même et la musique, que l’homme peut parvenir à la raison. Le véritable objectif des efforts éducatifs de Monge, Carnot, Dupin et des premiers grands Polytechniciens était de faire accéder de plus en plus de gens à la compréhension de ce processus afin qu’ils puissent le cultiver et en multiplier les bienfaits pour toute l’humanité. C’était là le secret, le secret totalement ouvert de leur mouvement destiné à « éveiller les lumières » dans tout le pays, et au-delà. Leur œuvre fut le fait de véritables républicains, dans le sens platonicien du terme, car élever la population à la moralité, voulait dire l’élever à la raison. À leurs yeux, moralité était synonyme de raison - n’oublions pas que le terme raison avait terriblement souffert dans ces années-là du rite jacobin qui avait réduit cette notion à une « déesse suprême », irréelle, froide et dérisoire.

En fait, ces républicains étaient des poètes. Dupin transmit cette conception de la géométrie supérieure dans un langage hautement poétique. La polémique d’Edgar Allan Poe sur le mathématicien et le poète dans sa Lettre volée est des plus pertinentes. Poe, un grand poète qui était aussi officier du renseignement de la République américaine sorti de West Point, l’équivalent américain de l’École polytechnique, y rend un hommage à Dupin qu’il dépeint sous les traits apparemment fictifs de son détective français. « C.A. Dupin », dont il fait le porte-parole de la méthode néo-platonicienne d’enquête à l’opposé de la méthode britannique de déduction. Dans la Lettre volée, Dupin montre que l’esprit supérieur, celui qui a défié les efforts empiristes de la police française en cachant la lettre dans un endroit qu’elle ne parvient pas à découvrir, ne peut pas être l’esprit d’un seul mathématicien mais seulement d’un mathématicien qui est aussi un poète. Carnot, lui, écrivit de vrais poèmes, que Prieur mit souvent en musique. Hyppolite Carnot dit de son père que lorsque ce dernier travaillait sur des problèmes militaires et scientifiques, il lui arrivait souvent de s’arrêter, de parcourir à grands pas son appartement, et de commencer à fredonner un poème qu’il notait au milieu de ses plans militaires ou équations. Ce principe poétique donnait lieu à de joyeuses festivités : Carnot était membre de la Société des Rosati à Arras, une société de poètes et d’amateurs de bon vin, qui se réunissait pour des banquets où se succédaient les poèmes et les pièces musicales. Ces réunions n’avaient rien de bacchanales : elles étaient la célébration de la créativité et de la raison humaines, comme dans Le Banquet de Platon.

Le dessin artistique s’était aussi vu attribuer une place importante dans le programme de l’École polytechnique, à côté des mathématiques, de la physique et de la chimie. Voici comment le célèbre peintre Neveu présentait son programme d’enseignement de cette matière :

« On parlera de la peinture en général (...) Dans sa définition la plus relevée, elle sera aussi l’art d’exciter des pensées par des sensations (9), d’agir sur l’âme par l’organe de la vue ; c’est par là qu’elle prend de l’importance, qu’elle rivalise avec la poésie, qu’elle peut, comme elle, éclairer les esprits, échauffer les cœurs, exciter et nourrir les sentiments élevés. On fera sentir les secours qu’elle peut prêter à la morale et au gouvernement ; comment elle sera dans les mains du législateur habile un puissant moyen pour inspirer l’horreur de l’esclavage, l’amour de la patrie, et conduire les hommes à la vertu. »

Neveu s’opposait à ce que les élèves se contentent d’« imiter » le dessin ou la peinture sans en comprendre la véritable signification. En étudiant le travail d’un peintre, l’élève devait au contraire s’élever et « grandir » avec le peintre. « La peinture, pour remplir l’idée qu’en ont toujours eue les hommes éclairés, doit s’élever à de plus hautes conceptions », disait Neveu contre l’imitation, « il faut qu’elle parle à l’intelligence (...) qu’elle élève l’imagination, qu’elle conserve de grands souvenirs, qu’elle fasse naître de grandes pensées (...) c’est alors qu’elle s’élève à toute sa dignité, qu’elle rivalise avec la poésie ». Les règles de la composition des plus grands tableaux (Léonard de Vinci était considéré comme le maître « universel ») étaient étudiées du point de vue géométrique le plus avancé, où science et art ne faisaient plus qu’un, dans ce qui fut en France la première présentation publique des « principes généraux de l’art » - l’art n’étant plus présenté comme enveloppé de « mystère » mais le fruit et la célébration de la mentation créatrice.

La géométrie naturelle est le génie lui-même « Il est une science simple, exacte, lumineuse, profonde, sublime : sa marche est lente, méthodique, circonspecte ; elle assure la possession du cultivateur, guide le navigateur au travers des écueils de l’océan, pèse les globes célestes, calcule leurs distances, décompose la lumière, connait la vitesse : c’est l’art d’Euclide ; mais il est une autre géométrie plus subtile encore, dont les principes sont pour ainsi dire le sentiment (Note). Fille de l’imagination et non de l’étude, à laquelle un jugement exquis, un coup d’œil prompt, un tact heureux servent de nombres, de règle et de compas, ses opérations sont métaphysiques, ses résultats s’obtiennent par un calcul rapide que des signes extérieurs ne peuvent représenter ; c’est elle qui guide l’artiste ingénieux, de qui l’art d’Euclide est souvent ignoré ; c’est la seule lumière qui nous reste, lorsque la marche ordinaire devient trop lente, les objets trop multipliés, les rapports trop compliqués ; elle aperçoit intuitivement, elle veut un génie aussi hardi que profond, plus vif que méthodique, plus vaste que réfléchi : sans cette géométrie, l’autre est un instrument inutile ; elle crée, l’autre polit ; elle est mère de l’invention, l’autre l’est de la précision. C’est à l’aide de ces deux flambeaux qu’Archimède éclaira l’univers (…). »

Note : C’est la géométrie naturelle, espèce d’instinct bien différent de la géométrie acquise. La science ne donne pas le génie, et la géométrie naturelle est le génie lui-même appliqué à la mesure des grandeurs. La géométrie acquise est, par son exactitude même, forcée à une lenteur extraordinaire, et bornée à des cas très simples. L’autre à un usage prompt, et s’applique à tout ; elle voit d’un coup d’œil ce qui gêne les combinaisons, sans influer sensiblement sur les résultats, et fait habituellement se relâcher d’une exactitude trop rigoureuse en faveur de la célérité ; c’est par elle que les mathématiciens entrevoient les résultats d’une hypothèse, avant même que de l’avoir analysée par un calcul exact, c’est aussi la géométrie qui est nécessaire aux généraux pour saisir en un instant la disposition, l’ordonnance et la marche des troupes.

Lazare Carnot, Éloge de M. le Maréchal de Vauban, 1784.

La philosophie de la science

« Les belles découvertes mathématiques ne sont jamais le résultat d’une combinaison mécanique et pour ainsi dire aveugle de signes abstraits. Il faut que l’esprit, pour me servir d’une belle expression de Montaigne, il faut que l’esprit par ses vues primesautières devance la marche matérielle des manipulations du calcul. C’est cette providence du génie, guidée par des règles plus ou moins sûres, par des inductions plus ou moins directes, et souvent par un simple pressentiment de ce qui doit être ou n’être pas la vérité, c’est elle qui constitue la philosophie de la science. »

Charles Dupin, Essai historique sur les travaux scientifiques et les services de Gaspard Monge, 1819.

Notes :

(8) Cf. René Taton, L’œuvre scientifique de Monge.

(9 De toute évidence, les « sensations » auxquelle